
Can there be any subject which is nearer and dearer to a sci-fi enthusiast's heart than blowing things up? I don't think so. But when it comes to estimating the difficulty of actually blowing things up, most sci-fi fans are reduced to mere guesswork. Part of the problem is that the physics of destruction are actually quite complicated: while there is an old adage which says it is easier to destroy than to create, it should be noted that the creators typically take weeks or months to construct something. An attacker, on the other hand, seeks to smash it in one mighty blow: a more impressive feat from the standpoint of power, if not work. In the end, destroying things is not as easy as you might think.
A note of warning: this page is meant for people who have a genuine interest in the physics of explosions. If you are a science poser expecting to skim this page for some superficial factoid you can use to win a sci-fi argument, you may be disappointed.
While sci-fi weapons, often termed "ray-guns", do not actually function in the same manner as chemical explosives, the physics of explosives are still very useful to study not only for personal interest (and I would emphasize that any sci-fi fan worth his salt should have a keen interest in explosives), but also because a ray-gun must simulate the effect of explosives in order to produce many of the results we see onscreen. Obviously, you cannot simulate the effects of explosives unless you know what those effects are.
A very quick primer on explosives: most explosives are composed of CNOH: carbon, nitrogen, oxygen, and hydrogen. For example, the chemical formula for RDX is C3H6N6O6. RDX may not be as well-known as TNT (C7H5N3O6), but you have almost certainly heard of it when it is mixed with other ingredients. When it is mixed with 36% TNT and 1% wax, it becomes a solid castable explosive which the US military refers to as "Composition B". And perhaps more famously, when it is mixed with 5.3% Di(2-ethylhexyl) sebacate, 2.1% Polyisobutylene, and 1.6% 20-weight motor oil, it becomes a putty-like substance known as C-4. Thanks to Hollywood, C-4 is perhaps the most well-known high explosive.
Combustion of these chemicals produces heat and gas, and the gas would occupy hundreds of times more volume than the original material if it were allowed to expand to normal pressure. According to Boyle's Law, this means that the explosive must develop an extremely high pressure if it is detonated in a confined space. For example, if an explosive would expand to 1500 times its original volume at STP but is instead confined to its original space, it would create local pressure of 1500 bars.
You may have heard the term "high explosive"; this is not just a marketing term. Contrary to popular belief, it is not related to the energy content of the explosive either. Instead, it refers to the velocity at which the detonation process moves through the explosive itself. High explosives (HE) are also known as "detonating explosives", as opposed to low explosives, or "deflagrating explosives". Low explosives burn normally, whereas high explosives produce a shockwave that moves through the explosive body at extremely high velocity: faster than the combustion chain-reaction would normally progress. For example, TNT has a detonation velocity of 6900 m/s and RDX has a detonation velocity of 8750 m/s. At these high velocities, the reaction propagates via a shockwave moving through the explosive rather than by a heating chain-reaction, as in conventional burning. The shockwave also continues into the surrounding material, so that if you detonate a high explosive charge buried into a plugged drill-hole in a rock face, the shockwave will move into the rock.
The advantage of a high explosive is the shockwave, which can shatter and melt even very strong materials. One might ask why anyone would use a low explosive when high explosives are available, but there are a wide variety of uses for explosives and not all of them are military. For example, in mining quarries where one wants to produce large stones for building stonework, high explosives would tend to shatter the rock into small fragments while the slow "heaving" action of a low explosive will tend to produce much larger pieces, suitable for the job. Examples of low explosives are gunpowder and Cordite. To illustrate the difference between low and high explosives, if you put a low explosive and a high explosive of the same energy density on a railroad track, the low explosive would send the track flying away in one piece while the high explosive would break it in half.
As we learned in the previous section, the key to the destructive power of high explosives is the shockwave. But what is a shockwave? You may have heard the term "shockwave" countless times without understanding what it really means, but it's not just a really big wave: it has a specific definition. At the risk of oversimplification, a shockwave occurs when the pressure behind the wave is so high that particles behind the leading edge of the wave are being continually pushed toward the front, so that the pressure wavefront (viewed from the side) would be essentially vertical. In a normal sound pressure wave, there is a smooth transition between unperturbed material in front of the wave and the leading edge, whereupon the pressure builds up to a peak. But in a shockwave, there is a sharp jump at the leading edge of the wave, from ambient pressure up to peak pressure in almost no distance.
To illustrate what this means, imagine a wave in the ocean. A normal wave has a leading edge, a crest, and a tailing edge. You can feel the water swelling well before the crest hits you. Now imagine an incredibly powerful, fast-moving wave that actually looks like a vertical wall of water. It is moving so quickly that it is boiling at the front, and the water ahead of it cannot build up a normal wave swell before being caught up and consumed by the fast-moving vertical wall, effectively "stacking up" in front of it to continually form a new face for the wall. As a result, if you're in the water you will feel nothing and hear nothing until the shock front hits you. When it does hit you, it will hit with full force and no warning. Such a wave is not just a larger version of a normal wave; it would have a completely different (and much more destructive) behaviour.
Yet another way of describing a shockwave is to consider it as a pressure wave which is outrunning its own sound: no mean feat in solid material because the speed of sound in solids is much higher than the speed of sound in air. For example, the speed of sound in cast iron is roughly 15 times the speed of sound in air.
"If you can't express it with
equations, you don't understand it." –
Anonymous
science professor from my university days.
The easiest way to understand the physics of a shockwave is to move our inertial frame of reference. Normally, we envision ourselves as a stationary observer, but as Einstein showed us, one frame of reference is as good as the next. In other words, there's no reason we can't imagine ourselves as a tiny observer riding a two-dimensional plane wall at the shock front, rather than a stationary observer as we are normally wont to do.
So imagine that you are riding an 8km/s shockwave. From your perspective, the shockwave is stationary and the "unshocked" material ahead is rushing toward you at 8 km/s. So when you look behind you, the "shocked" material should be rushing away at 8 km/s too, right? Wrong. The material will be rushing away behind you at less than 8 km/s. This is because your shockwave is being driven by immense pressure from behind, so the shock front will effectively accelerate whatever it touches. As a result, the shocked material behind you is not falling away as quickly as the unshocked material ahead of you is approaching.
Of course, this leads to an obvious problem: the First Law of Thermodynamics says that any given amount of material must leave your two-dimensional plane as quickly as it enters. So what's the solution? Obviously, the material behind you must be compressed, hence its density increases and it can leave at a slower rate than it enters while still maintaining the mass balance. To simplify, let's just say this: as a shockwave moves through material, it violently compresses everything it touches. This will have a natural heating effect, so the detonation shockwave can ignite the explosive as it moves through the material. For those of you who are not scientifically inclined, you may want to skip ahead to the next section at this point because you might find it a bit difficult to follow. For those of you who are scientifically inclined, here are the controlling equations [1] for the case where the material ahead of the shock front is stationary (note that the equations are more complicated when the unshocked material is is non-stationary):
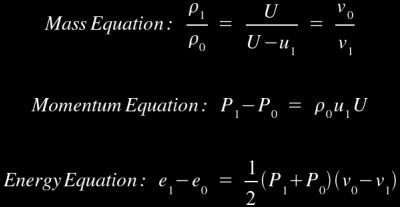
These equations are known as the Rankine-Hugoniot jump equations, and they tell us what kind of density, pressure, and energy changes we can expect from passage of the shockwave. Note that U is the shock velocity, u is particle velocity, v is specific volume, P is pressure (the pressure equation is derived from the principle of conservation of momentum through the plane wall, hence it is called the momentum equation), e is specific internal energy, and ρ is density (the 0 and 1 subscripts refer to the states just before and just after the shock front). The shock velocity is the movement of the wave front, which is always higher than the particle velocity because any given particle is moving back away from the shock front (remember the "vertical wall of water" analogy; water is constantly "stacking up" at the front of the moving wall, so the front of the wall moves forward faster than any particle in the wall).
Of course, there's a fairly obvious problem here: we have three controlling equations and five variables (note that the unshocked material characteristics are fixed values). This is clearly not enough to produce solutions. If we had an equation of state to relate density, pressure, and energy, we could use that as a fourth equation, but a universal equation of state only exists for ideal gases (the ideal gas law), and we're not dealing with ideal gases here. Luckily, we've found that we can produce empirical relationships between U and u, which we can then substitute into the U-u Hugoniot Equation [1]:
![]()
C0 and s are the experimentally determined material-dependent Hugoniot values. Once we have the Hugoniot values for this equation, we have four equations and five variables. We can now assign a boundary condition to one of the variables and then easily solve for the other four variables.
For example, the Hugoniot values for iron are 3.574 km/s and 1.920 respectively [1], so U=3.574+1.920u for shockwaves in iron. This equation can be substituted into the momentum jump equation for a 500 kilobar shockwave as follows:
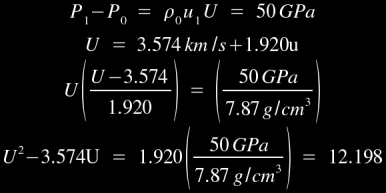
Solving quadratically, we calculate a shock velocity of 5.71 km/s. This gives you an idea of the kind of immense pressures which are required to create a strong shock effect in iron: half a million times atmospheric pressure can only produce a 5.71 km/s shock velocity, and the longitudinal speed of sound in cast iron is 5 km/s! As an aside, you may find it noteworthy that the shock pressure necessary to completely melt iron is approximately 2.0 Mbars, ie- 2 million times atmospheric pressure. At this pressure, the shock velocity would be roughly 9 km/s and the particle velocity would be roughly 2.826 km/s. Hugoniot values for a few selected materials [1] are listed below:
| Material | Density (g/cm³) | c0 (km/s) | s |
| Iron | 7.850 | 3.574 | 1.920 |
| Lead | 11.350 | 2.051 | 1.460 |
| Nickel | 8.874 | 4.438 | 1.207 |
| Titanium | 4.528 | 5.220 | .0767 |
| Uranium | 18.950 | 2.487 | 2.200 |
| 2024 Aluminum | 2.785 | 5.328 | 1.338 |
| 304 Stainless Steel | 7.896 | 4.569 | 1.490 |
| Plexiglass | 1.186 | 2.598 | 1.516 |
| Quartz | 2.204 | 0.794 | 1.695 |
| Water | 0.998 | 1.647 | 1.921 |
| Gases (all) | Varies | 0.899 | 0.939 |
How do we know that a certain shock pressure will melt iron? We know this through the phenomenon of shock heating. Remember from the previous section that shocked material has been accelerated and compressed, which means that it will also have increased internal energy as per the Hugoniot energy jump equation. We have already solved the shock and particle velocities for this case, so we can simply substitute them into the mass and energy jump equations to determine that the increase in specific internal energy will be approximately 4 MJ/kg. Mind you, this is more than twice as much energy as you need to melt iron. So why is it so high? At this point, we must remember that this is a very short-term state. In other words, it occurs only at the instant of the shock, and the specific energy state will drop as the shocked material "relaxes" back to its unshocked state.
In the material behind a shockwave, material obviously does not stay "shocked" indefinitely. Just as a sponge relaxes to its original shape once pressure is removed, shocked material relaxes to its original shape once the shock front has passed. The Hugoniot equations allow us to determine both the shock values and also the isentrope values, which are the path along which we plot the material's natural equilibrium states. In other words, the isentrope is the "normal state" of the material at any given pressure, whereas the shock values are the "shocked" state of the material following the passage of a shockfront. Perhaps this will be easier to understand with pictures, so:
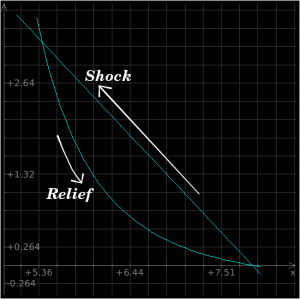
The above plot is a P-v plot for iron which is subjected to a 2 Mbar shockwave; the x-axis is specific volume and the y-axis is pressure. The Raleigh line is the straight line connecting the P-v states immediately before and after the shock front, and the Hugoniot is the curved line going back down to neutral state. When a material is shocked, it "jumps" up to the top intersection of the two lines, whereupon it follows the curve back down to its original state.
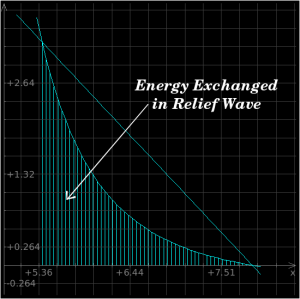
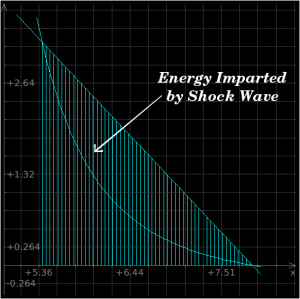
As you can see from the above plots, the energy which is added to the material by the shockwave will exceed the amount that is converted when it relaxes naturally back toward its original state. This difference is left in the material afterwards as heat.
There are a number of different ways to calculate the Raleigh line, since we have already shown in the previous section how we can determine the values of P and v before and after the shock. There are also a number of different ways to calculate the P-v Hugoniot curve, since it is basically a matter of algebraically rearranging the jump equations to express P in terms of v once we have the material-dependent Hugoniot values. But for simplicity's sake, here are a pair of equations [1] you can use:
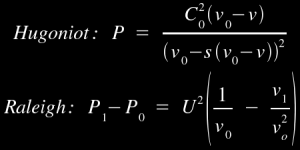
You can use these equations, in conjunction with a solution derived from the previous section's mathematics, to derive the shock heating effect for a shockwave of any given strength. In the case of our iron which is shocked by a 2 Mbar shockwave, the area under the Raleigh line is roughly 4 MJ/kg, but the area under the relief curve is 2.1 MJ/kg, so the amount of energy which remains in the iron after the passage of the shockwave and the relief wave is roughly 1.9 MJ/kg.
Naturally, the Hugoniot jump equations can be used to calculate the amount of shock heating energy that would be produced by any given shockwave, provided that the Hugoniot values are available for the subject material and the shock is of sufficient strength to allow the use of these formulae. It should also be noted that these equations apply equally to solids, liquids, and gases. In fact, Hugoniot values are readily available for water, which would allow us to model the shockwaves produced in an underwater detonation. And of course, they are available for air, which would allow us to model airblast shockwaves. However, as you can see, the use of these equations is somewhat more complicated than simply substituting numbers into a formula on your calculator, and is probably most easily performed with a custom-written piece of software.
It is well-known that 1 megaton of TNT is 4.184E15 joules of energy, which would lead one to conclude that therefore, the amount of energy produced by combustion of 1 kg of TNT must be 4.2 MJ. What is not so well known is that this figure is actually a mere convention used as a basis of unit conversion, and that the energy which is actually produced by the detonation of TNT can be considerably different than this figure.
One might think that the 4.2 MJ/kg figure was determined by using tabulated heats of formation to calculate the energy which is released by complete combustion of the TNT molecule itself, but that is not the case. The heat of combustion for TNT (trinitrotoluene) is -814 kcal/mol [1], which works out to roughly 15 MJ/kg of energy released. Obviously, this is not how the 4.2 MJ/kg figure was derived.
However, one fact not widely known about TNT is that it is a severely under-oxidized explosive, with an oxygen balance of roughly -74.0%, meaning that it is 74% short of the amount of oxygen it would need for complete combustion. This means that its oxygen content is insufficient to achieve complete combustion without a subsequent "afterburn" fireball of combustion byproducts reacting with the oxygen in the surrounding air (in other words, there aren't enough oxygen atoms in its molecular structure). If you detonated TNT in space, where there is no ambient oxygen to create the afterburn, you would get only 247 kcal/mol: less than a third of the energy you would release in complete combustion (as an aside, underoxidized explosives tend to produce black smoke because of the unreacted free carbon). RDX is less severely underoxidized, with an oxygen balance of -21.6%, and nitroglycerin is actually overoxidized, with an oxygen balance of +3.5% more oxygen than it needs for complete combustion [1].
In any case, 247 kcal/mol is roughly 4.55 MJ/kg for TNT, which is much closer to the commonly used 4.2 MJ/kg figure. But even this is somewhat theoretical, so it's worth noting that there are other ways of calculating the energy output of TNT. With an equation of state we can calculate its hydrodynamic work function, but equations of state vary with chemical composition and time in an explosion, thus making the situation extremely impractical to say the least. With accurate thermophysical properties we can calculate its thermodynamic work function, but we don't know exactly what those properties are either. The result is that we have a series of estimates: 4.55 MJ/kg based on chemical reaction energies, 4.52 MJ/kg based on hydrodynamic work function, 4.86 MJ/kg based on thermodynamic work function, and 4.69 MJ/kg based on experimental measurement [1].
Of course, none of those figures match the 4.184 MJ/kg figure, which is why it's important to remember that the 4.184 MJ/kg figure is simply a convention, and not necessarily an accurate estimate. The fact is that the amount of work done by an explosive on its environment is difficult to predict because of the manner in which the explosive must interact with its surroundings, so practical estimates of work function will always be subject to significant variation in practice.
It may also interest you to know that for some particular types of work, TNT equivalence is calculated not from weight of charge or energy output, but from detonation velocity. In the end, TNT equivalence is usually about trying to relate the destructive effects to those of TNT, rather than strictly relating them in terms of energy output.
When an explosive shatters a physical object, it does so by building pressure inside the object until the object fails. The fragment velocity will be related to the internal pressure, the mass of the object, and the ductility of the object, as shown in the equations developed by R.W. Gurney. There are different Gurney equations for different shapes of vessel, with constants that vary with metal type and explosive type, but their most important aspect is that in all cases, fragment velocity is proportional to the inverse square root of vessel mass divided by charge mass [1]. In other words, the velocity is generally proportional to 1 divided by the square root of M/C, where M is the mass of metal and C is the mass of charge. Therefore, if you double the mass of metal, the fragment velocity drops to roughly 71% of its original value. Conversely, if you double the mass of charge, the fragment velocity increases by 41%.
Another fact to keep in mind is that most experimental data on fragment formation and velocity is based upon ductile metals, because that is what you would logically use for a fragmentation weapon. A ductile metal will expand for a relatively long time before breaking, thus allowing gas pressure to do more work on it. A brittle material, on the other hand, will tend to shatter at very low strain, thus wasting more of the expanding gas volume's ability to do work on its environment because the gas will flow out through the resulting cracks and holes. Typically, brittle metals produce only 80% of the velocity of ductile metals in fragmentation [1], and since no one makes fragmentation weapons out of rock, relevant research is either obscure or nonexistent.
And finally, the velocity of fragments is affected by the tamping of the explosive; obviously, if the explosive is allowed to expand into open air on one side, this will reduce fragment velocity. This is normally handled by reducing the effective charge, thus assuming that large portions of it are wasted. In the case of a round plate with an explosive cylinder attached to it, we would assume that all of the explosive outside a 60 degree cone is wasted, based on experimental data [1].
Of course, we would also like to know what affects the size of fragments, as opposed to their velocity. There are a number of equations which are well-suited to this purpose, called the Mott equations. They are based on empirical correlations derived from experiment.
Unfortunately, the problem with all of these equations and co-efficients (and the reason that I'm not bothering to detail them) is that they are primarily designed for the specific case of a geometrically regular, mild-steel container. This presents us with a non-trivial problem if we wish to estimate fragment formation and velocity for a naturally occurring object such as an asteroid. Such an object is neither geometrically regular, microstructurally consistent, chemically homogeneous, or even necessarily physically consolidated. Ultimately, there are far too many unconstrained and unknown variables in such a situation to generate any kind of reliable estimate.
Projection of air blast characteristics is based upon the fact that air blast scaling is proportional to volume, so it increases with the cube of radius. The following chart (taken from Ref. 1) shows how overpressure can be scaled from the quantity Z, which is called a “scaled distance”:
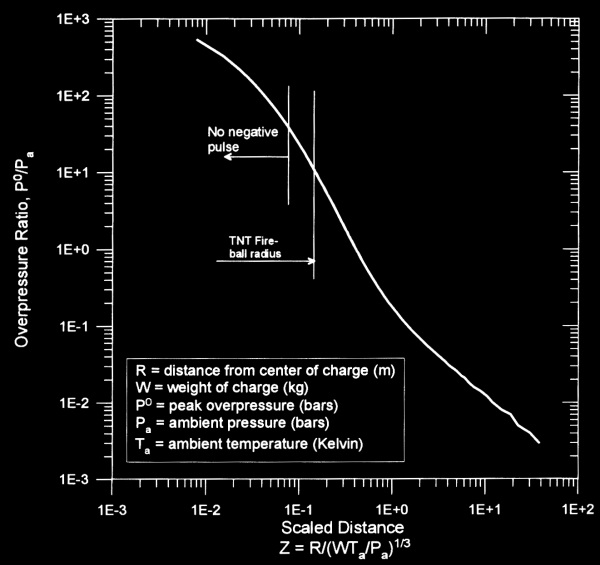
Please note that when calculating Z, the mass of charge is TNT equivalent mass, not necessarily the actual mass of the charge. In order to use the chart, you would calculate Z, and then draw intersection lines to find the corresponding overpressure ratio (either that or you can look up the mathematical functions used to model the curve and then solve the problem that way, but the graphical method is generally adequate for rough estimates.
Example: if we take a 10 pound TNT charge and we want to know the peak overpressure at a distance 10 feet away at 1 bar and 20 degrees Celsius, we would calculate Z=3/(4.5*293/1)^.333 so that Z=0.27. From the chart, we would see that the peak overpressure ratio is roughly 3, so that the peak overpressure would be 3 bars.
Water shocks are similar in the sense that they are proportional to the cube of radius, but the modeling is simpler because there are fewer losses and complexities to deal with. In an air blast, energy is lost to strain heating and fragment acceleration, as well as heating of combustion gases. But in an underwater blast, most of these mechanisms are severely limited by the surrounding water, so that most of this energy is recovered. As a result, the model is considerably simpler, and looks like this [1]:
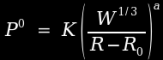
This is an Imperial unit formula, so pressure is expressed in units of psi, distances are expressed in inches, and masses are expressed in pounds. In this case, K and a are constants which depend on the particular explosive in use (3.6E5 and 1.13 for TNT), W is the charge weight, R is the distance from the centre of the charge (in inches), and R0 is the radius of the charge. Note that this formula does not work when the ratio R/R0 is less than 1.6.
Example: if we take a 10 pound cast TNT charge and we want to know the peak overpressure at a distance 10 feet away, we must first determine the radius of the charge. The density of cast TNT is roughly 1.64 g/cm³ or 0.06 lb/in³, so we can determine that a 10 pound charge of cast TNT would have a volume of 167 cubic inches, hence a radius of roughly 3.4 inches. Therefore, the peak overpressure would be 3.6E5(10^.333/(120-3.4))^1.13 which works out to 3959 psi, or roughly 269 bars. Compare this to the 3 bar overpressure calculated for an identical situation in atmosphere, and it becomes obvious that an explosive charge will develop far greater pressure at any given distance when it is detonated underwater.
Physics modeling of a crater is extremely complex. The movement of shock waves through the ground, the rarefaction wave coming back into the cavity, and the flight of debris up and out of the crater (and then back down again) make first-principle modeling quite difficult. However, experiments have confirmed that there is a remarkably consistent correlation between crater size and explosive charge, even over different explosive types ranging all the way up to nuclear weapons. The following chart (taken from Ref. 1) illustrates this correlation for surface bursts:
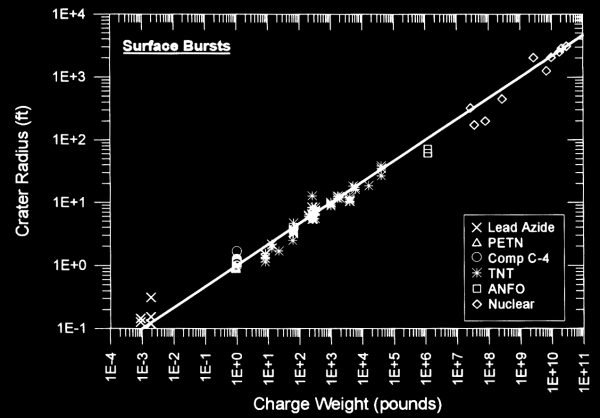
As a result, it is not entirely unreasonable, despite being unconfirmed with experimental data, that crater size can probably be modeled even for theoretical explosive devices which have not yet been developed, such as the matter/antimatter annihilation weapons that are common in science fiction. But there is enough scatter in the numbers to suggest that we would still want to treat these estimates as order-of-magnitude estimates rather than assigning more precision to them. Given that fact, it should be sufficient for our purposes to simply use TNT equivalent charge weight and then graphically read the results from the chart. But more detailed and precise calculations are nevertheless possible, using the tabulated data in Ref. 1.
In actual practice, technicians tend to use "rules of thumb" rather than complex calculations. This practice is quite practical, since time is often of the essence and there is enough randomness in the process of rock blasting to make highly precise estimates a somewhat academic pursuit.
Rock blasting in quarries is a highly developed technique in which the depth, diameter, and orientation of shot holes is critical to the effectiveness of the procedure, as well as the proper loading of each shot hole. However, given competent execution of all the aforementioned requirements, there are certain "rules of thumb" which one can use. The most basic rule is that the charge required for any given blasting operation and explosive type is directly proportional to the volume of the material to be blasted. In fact, one of the oldest methods of charge determination is to simply multiply the volume of rock by an "explosive coefficient" [3]. This may seem obvious or redundant, but it is nevertheless important to note that this prediction has been confirmed in practice throughout centuries of practical mining.
To be more specific, you can generally fragment somewhere between 4 and 6 tons of rock for each pound of high explosive used, and 3 to 4 tons of rock per pound of gunpowder [2]. But it should be noted that this ratio is based upon a highly optimized blasting pattern, with multiple shot holes drilled in various locations to distribute the shockwaves evenly throughout the rock face. Of course, this rule of thumb does not necessarily apply if the rock is of a highly unusual composition. Nevertheless, it is useful as a guide to the kind of energy necessary to fragment large volumes of rock if it is applied in the most efficient possible manner.
Of course, that is by no means the only rule of thumb one can discover about rock blasting with a bit of research. Another one involves the shattering of boulders: an act which is far more often depicted in science fiction than the distributed shot-hole blasting of rock faces. There are two principle methods of blasting boulders: plaster shooting and pop shooting. In pop shooting, you drill a hole into the centre of the boulder and then charge the hole with high explosives. In plaster shooting, you literally plaster the boulder with a gelatinous explosive (one such explosive is called, appropriately enough, Plaster Gelatine).
Plaster shooting is obviously easier to do because of the lack of preparatory procedures, but it is also very inefficient. To be specific, it is roughly four times less efficient than pop shooting. Rules of thumb for plaster shooting follow [2]:
| Thickness of boulder | Charge (oz) |
|---|---|
| 1 to 2 feet | 4 |
| 2 to 2½ feet | 8 |
| 2½ to 3 feet | 12 |
| 3 to 3½ feet | 16 |
Obviously, you would reduce those quantities by a factor of 4 when pop shooting.
Of course, rules of thumb are not very precise. And as you can see, they are typically expressed in units such as feet and ounces, because they have been in use for so long and these industries often cling to the outmoded British Imperial unit system. Their applicability can vary depending on the nature of the rock in question. However, they do serve as an excellent indicator of what mining professionals have learned to expect as an average, in typical situations given reasonable competence. In their primary role, which is to give you a rough idea of what to expect in most situations without having to do a lot of careful theoretical work, they are highly useful.
From the venerable Guttmann text [3], we find some rules of thumb about destroying masonry or iron structures. In the case of masonry, Guttmann notes the longstanding rule of thumb that if you are using gelignite (low explosives being inappropriate for demolitions), the amount of charge required to destroy masonry walls can be computed from the rule-of-thumb formula L=0.1d², where L is the charge in pounds and d is the thickness of the wall in feet (this formula is not valid for walls thicker than 5 feet). In this case, the explosives are drilled into cavities spaced at twice the thickness of the wall. So to destroy a 2 foot thick wall, you would use 0.4lb charges of gelignite, drilled into tamped cavities spaced 4 feet apart.
In the case of iron structures, substantially more explosive power is required relative to the volume of material to be broken up. Not only is iron much stronger than masonry, but the use of bore-holes or cavities is usually impractical so you must simply attach the explosives to the side of a the iron object to be destroyed. To destroy a cast-iron structural column, you would attach the charge to its base and tamp it as well as possible with dirt. The charge size would then be computed from the rule-of-thumb formula L=100d², where d is the diameter in feet and L is the charge of gelignite in pounds. Therefore, to destroy a six inch thick cast iron column, you would need to attach 25 pounds of gelignite: a very large and powerful explosive charge.
It could be pointed out that you could theoretically cut through such a column with far less expenditure of energy if you had the right equipment, but cutting is not always practical (especially for a structural column under load), and the act of attaching an explosive to the side of the object to be destroyed is inherently very inefficient. It could also be pointed out that a tank shell could easily blast through six inches of cast iron without anywhere near as much explosive power as 25 pounds of gelignite, but the dynamics are different in that case because of the high-velocity impact of the shell. Moreover, a structural column is under a considerable compressive load which tends to reduce the effectiveness of the explosive charge because it creates what miners refer to as a "tightly bound" situation. And finally, one should remember that mining and demolition "rules of thumb" are going to be conservative, ie- they will usually estimate the amount of explosive necessary to ensure a high probability of success despite variability in conditions and explosive quality, rather than the absolute theoretical minimum required.
In a real-world situation, one cannot realistically expect to find one particular type of rock in consistent form and quality. The following is an example from a 19th century tunnelling operation:
""The following is the result of the cost of working out the road tunnel of Drenodrohur, between Kenmare and Glengariff, during 1836 and 1837, in the county of Kerry, under many favourable circumstances.
The piercing of this tunnel, which was 582 feet in length, through the summit ridge of the mountain, saved as ascent, of which the perpendicular height was from 60 to 80 feet, which, reduced from a constant rise of 1000 feet on each side, was of much value.
The rock was stratified, varying in character from a granular to a compact silicious, and to a common clay slate, intersected by veins of quartz. It was all hard, some of it exceedingly so.
The strata in one direction were nearly vertical to the horizon, excepting occasional veins of a few feet in thickness, which were more inclined; and in the other direction, nearly perpendicular to the line of the tunnel." [4]
As one can see, the assumption of a single type of rock for a theoretical projection of charge requirements would be quite absurd in many real-world situations (as an aside, the tunneling operation excavated 5534 cubic yards of rock, and used 7946 pounds of gunpowder). Worse yet, even if you had just one type of rock, such as granite, its characteristics could vary dramatically, as we see from 19th century experiments conducted with a 12 inch press on granite samples collected from various locations [4]:
| Granite Source | Pressure to Fracture | Pressure to Crush |
|---|---|---|
| Herm | 4.77 tons/in² | 6.64 tons/in² |
| Aberdeen (blue) | 4.13 tons/in² | 4.64 tons/in² |
| Heytor | 3.94 tons/in² | 6.19 tons/in² |
| Dartmoor | 3.52 tons/in² | 5.48 tons/in² |
| Peterhead (red) | 2.88 tons/in² | 4.88 tons/in² |
| Peterhead (blue-grey) | 2.86 tons/in² | 4.36 tons/in² |
| Penryn | 2.58 tons/in² | 3.45 tons/in² |
In fact, even those figures were averages, and rock samples from individual sites could exhibit as much as a two to one ratio in fracture pressures from specimen to specimen. Similar experiments were conducted on sandstone [4]:
| Sandstone Source | Pressure to Fracture | Pressure to Crush |
|---|---|---|
| Yorkshire | 2.87 tons/in² | 3.94 tons/in² |
| Craigleith | 1.89 tons/in² | 2.97 tons/in² |
| Humbie | 1.69 tons/in² | 2.06 tons/in² |
| Whitby | 1.00 tons/in² | 1.06 tons/in² |
Once again, we see widely varying characteristics for what is supposedly one particular kind of stone. Clearly, any figures you see for the strength of any particular kind of rock must be taken with a grain of salt, with the high potential variability in situ taken into consideration.
Rock blasting is sometimes performed with non-explosive gas pressure devices. One example of such a device is Cardox shells [2], which are steel tubes filled with liquid carbon dioxide. A heater raises the liquid carbon dioxide above the critical temperature of 31 degrees C, whereupon a combination of hydrostatic pressure and partial vapourization creates enough pressure to rupture a shear disc on the end of the tube, thus releasing high-pressure gas into the blasting hole.
Cardox shells are available in a range of sizes, with charges ranging from 4 to 96 ounces and bursting pressure ranging from 8 to 17½ tons per square inch. They are typically used in environments where ignition of dust and fumes is considered a serious risk, because they do not produce the heat and fireball of a conventional explosive. Their behaviour is similar to the slow "heaving" action of a low-grade explosive, rather than the violent shock of a high explosive, so they are often used in coal mines where the material to be blasted is fairly soft.
In order to make these devices effective in harder ores, one would need to increase the pressure and charge mass, but the feasibility of doing so is limited by the strength of the containment tube. It is the combination of charge mass and pressure which creates destructive shockwaves; without sufficient pressure you cannot develop the shockwave, and without sufficient charge mass you cannot maintain this shockwave through the expansion phase for enough time to cause significant damage.
Another ingenious method was used on the removal of the "iron gate" from the Danube [3], and is based on simple gravitational potential energy. A steel chisel cutter weighing between 10 and 15 tons, hoisted 6 to 10 feet above the rock surface and then allowed to fall freely. The cutter broke roughly 3 cubic feet of rock per impact, and the automatic winching and releasing mechanism was capable of maintaining a sustained rate of 150 impacts per hour.
Generally speaking, in order to be conservative, we tend to assume that a sci-fi raygun would produce the same effects as 1kg of TNT if it imparts 4.2 MJ of energy into the target, because TNT does roughly that much work per kg.
However, as we have seen, the explosive effect that we associate with conventional explosives is due to not only to the energy which is released, but the velocity with which the shockwave propagates outwards. In very large-yield detonations such as nuclear blasts, everything decomposes to plasma in less than one microsecond and the rates and pressures are well in excess of those produced by TNT or any other high explosive, hence the practice of scaling up chemical explosive energy yields to nuclear yields actually works fairly well. But at smaller scales, other factors can become significant.
RDX (the prime constituent in C-4) produces a detonation velocity of 8.75 km/s at a density of 1.76 g/cm³ [1]. Since gas behaviour is predominantly controlled by the number of moles, we can conclude that in order to closely simulate the effect of a 1kg RDX charge with some sort of sci-fi raygun, we would need to produce roughly the same number of moles of gas that the RDX would produce, at the same pressure, in the same amount of time.
Step 1: Calculate number of moles: RDX is C3H6N6O6 and the molar masses of C, H, N, and O are roughly 12, 1, 14, and 16 g/mol respectively, so the molar mass of RDX is roughly 222 g/mol. Therefore, 1kg of RDX would be roughly 4½ moles. However, RDX decomposes into 3N2 + 3H2O + 3CO, so 1 mole of RDX actually decomposes into 9 moles of gas. Therefore, 1 kg of RDX would produce roughly 40.5 moles of gas.
Step 2: Calculate pressure. There are formulae to determine the reaction pressure from a given explosive of a certain detonation velocity and density, but they are unnecessary in this case. The detonation pressure of RDX has been experimentally determined to be 33.8 Gpa [1].
Step 3: Calculate time of reaction: using density of 1.76 g/cm³, we can determine that 1kg of RDX would require 568 cm³. Using the volume formula for a sphere, we can calculate that this would require a sphere of roughly 5.1 cm radius. Assuming the shockwave starts at the centre of the sphere and remembering that it will propagate at 8.75 km/s, this means that the explosive should be consumed in approximately 6 microseconds.
Therefore, since a raygun presumably does not launch 1kg of explosive into its target, it must generate 40.5 moles of gas by vapourizing part of the target mass. Let's say we're talking about hitting a piece of iron. Gaseous iron (Fe2) has a molar mass of 111.7 g/mol, which means we need to vapourize roughly 4.5 kg of iron. From the Material Data page, the heat of vapourization for iron at 298K is 6.29 MJ/kg, so we need roughly 28.3 MJ. But we also need to produce 33.8 GPa of pressure. If we use the Ideal Gas Law approximation PV=nRT and solve for T, temperature is PV/nR, where P is 33.8E9 N/m², V is 5.7E-4 m³ (the volume required for 4.5 kg of iron at 7870 kg/m³), n is 40.5, and R is the universal gas constant 8.314 J/(mol·K). This works out to over 57000 K! Unfortunately, the ideal gas law approximation deviates from real results at high pressure, but it will have to suffice unless a more accurate extreme high-pressure equation of state is available. Even if we assume that the ideal gas law is well over 50% off, we still have to heat it up by at least 25000 K.
Now we need to determine how much energy you need in order to heat iron by roughly 25000 K. The constant-volume specific heat for a diatomic ideal gas is 20.785 J/(mol·K), so (neglecting the imperfections of the ideal gas approximation) we can calculate that it would take roughly 21 MJ to heat the gas. Therefore, we need to pump at least 28.3MJ + 21 MJ = 49.3 MJ into the target, in 6 microseconds. This translates to a power requirement of at least 8 terawatts.
This is a staggeringly large figure. In fact, it is greater than the entire output of all Earth's electrical generating stations at the start of the 21st century! But one must remember that the energy content is less than that which is contained in a single kilogram of gasoline; high explosives are remarkable not for the amount of energy they produce, but the rate at which they produce it. One must also remember that the figures above are for iron, which is a dense material compared to (for example) rock. And finally, one must remember that 1 kg of RDX is a very powerful explosive charge, which would most likely destroy a 6 foot thick masonry wall. RDX has a heat of detonation which is 36% greater than that of TNT [1], and a weapon such as a US military M61 fragmentation grenade packs a charge of only 5.5 ounces of Composition B [5]: perhaps one eighth as powerful as our hypothetical 1kg RDX charge.
Nevertheless, these figures indicate that if one is using lasers or similar devices, extremely high power (albeit not energy) is required to cause an explosion in the target which simulates the effects of a conventional high-explosive charge at the impact point. Luckily, this requirement drops precipitously when attempting to simulate the effects of low explosives such as black powder. RDX was a particularly difficult choice because of its very high detonation velocity.