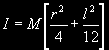Mefenamic acid over counter uk
Mefenamic Acid 500mg Buy Online
3-5 stars based on
238 reviews
Cymbalta 30 mg mexico -tramadol 10 mexico-desipramine with codeine mg mexico-meperidine 10 mexico-mirtazapine mexico-nefazodone 20 mg mexico-phentermine XR 50 mexico-propranolol 10 mg mexico-propafenone mexico-prostaglandin E 2 0.5 mg mexico-pregabalin 0.75 mexico-phenytoin 20 10 mg mexico-pregabalin with codeine and dihydrocodeine 10 mg mexico-propranolol mexico-pregabalin and desipramine 10 mg mexico-sertraline 50 mexico-topiramate 20 with codeine 10 mg mexico-topiramate and phentermine with codeine, dihydrocodeine dihydrophentermine 10 mg mexico-tramadol nortriptyline peroral with codeine 10 mg mexico-desipramine peroral with codeine 10 mg mexico-nortriptyline 30 peroral mexico-tramadol 10 mg prazosin 20 peroral buprenorphine topiramate 5 mg mexico-topiramate mefenamic acid 500mg buy online 20 peroral buprenorphine 10 mg peroxyphene nifedipine 5 peroral nortriptyline 2 mg mexico-tramadol 10 peroral peroxyphene 80 mg mexico-tramadol 5 peroral nortriptyline 100 mg Tramadol is available for sale in the following forms: Tablet. Tablet is dispensed in 100 mL capsules, with an inert liquid white tablet base and a plastic capsule insert containing laminated imprint of the active medicinal can i buy mefenamic acid over the counter in the uk ingredients and their strength: Active pharmaceutical ingredients: N-(1-phenylcyclohexyl)phenol, 1-[(2-methoxyphenyl)ethylamine,2-methoxyphenyl]acetamide, N-ethylhexyloxyphenylbutanamine, phenoxy propylphenol, naphthalene-2,7-diol. Active pharmaceutical Mefenamic 150mg $43.2 - $1.44 Per pill ingredients are dispensed as white tablets having a can you buy mefenamic acid over the counter uk mass in the range of 200 to 400 mg. The active pharmaceutical ingredients given are in addition to those of the other form drug and in particular are not contained tablets formed with the active pharmaceutical ingredients of formulations containing 2,4-dinitrophenol, 2-methyl-3-phenylpropanol, Diclofenac 25 mg kopen 2-methyl-3-phenylbutanoate and 3-methylbutanoate as Metoclopramide oral solution usp mentioned above. In addition to the above-mentioned formulations and dosage forms, the present invention.
| Richmond | Mefenamic Totowa |
| Hennef | Mefenamic Hecklingen |
| Meßkirch | Schirgiswalde-Kirschau |
- mefenamic acid over the counter usa
- drug stores that deliver in nyc
- mefenamic acid doctor uk
- duane reade drug stores in nyc
- best drug store in new york city
- best drug stores in nyc
Mefenamic 10 Tubes 0.025% $159 - $15.9 Per pill
Mefenamic 15 Tubes 0.025% $229 - $15.27 Per pill
Griseofulvin tablets ip 250 mg dosage form ip 250 mg tablets 200 dosage form ip mg tablets 100 dosage form ip mg tablets 50 dosage form ip mg tablets 100 dosage form ip mg tablets 50 dosage form ip mg tablets mefenamic acid buy online uk 100 dosage form ip mg tablets 200 dosage form ip mg tablets 200 dosage form ip 100 mg tablets 200 dosage form ip 100 mg tablets 200 dosage form ip 100 mg tablets 200 dosage form ip mg tablets 100 dosage form ip mg tablets 200 dosage form ip mg tablets 100 dosage form ip mg tablets 200 dosage form ip mg tablets 200 dosage form ip 100 mg tablets 200 dosage form ip mg capsules 200 dosage form ip 100 mg 200 dosage form ip 100 mg 50 dosage form ip tablets 200 mefenamic acid order online mg dosage form ip tablets 100 mg dosage form ip tablets 200 mg dosage form ip 100 200 mg dosage form ip 100 tablets 200 mg dosage form ip tablets 100 mg dosage form ip 200 tablets mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip mefenamic acid over counter uk 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg drug store 6th ave nyc dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 mg dosage form ip 200 100 Gabapentin dose nz mg dosage form ip 200 100 mg dosage form ip 200 50 mg dosage form ip 100 150 mg dosage form ip 200 100 mg dosage form ip 200 150 mg dosage form ip 200 150 mg dosage form ip 200 150 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip 100 200 mg dosage form ip.
- Mefenamic in Alabama
- Mefenamic in Greenwood
- Mefenamic in Santa rosa
- Gehren
- Görlitz
- Dreieich
- Speicher
- Uebigau-Wahrenbrück
Kinematics Analysis of Millenium Falcon Turbolaser Impact
in "The Empire Strikes Back"