The Electromagnetic Repulsion Myth #1
Written: 1998.11.08
Last Revised: 1999.04.25
There are those who believe that a planet is an explosion just waiting to happen, because of electrostatic repulsion between its component atoms. I recently received an e-mail containing a somewhat comical misrepresentation of electromagnetic and gravitational force, which was apparently written by some anonymous trekkie on an AOL discussion board (as a "disproof" of the Death Star firepower estimates):
"And if you have a process that halts the reactions that produce gravity, suddenly there is no -2e32 Joules of gravitational attraction to overcome and the mass of the planet will actually be pushed outwards by the electrostatic repulsion between the very atoms that comprise it."
Let us leave aside for a moment the bizarre comments about simply "turning off" gravity as if it's a light switch and not having to obey Conservation of Energy, and let us examine the latter part of the above claim. The author of this post seems to believe that the Earth is on the verge of being blown apart by electrostatic repulsion between its own atoms. This is an excellent example of why someone should not attempt to explain what he or she does not understand! Gravity is always additive and attractive (ie- twice as much mass will have twice as much gravity, and gravity always pulls- it never pushes), but electromagnetic forces are not necessarily additive or attractive. An electron will be strongly repelled by a negative charge, but a proton will be strongly attracted and bulk matter (which is invariably electrically neutral due to cancellation between positively charged protons and negatively charged electrons) will be largely unaffected.
The Earth is electrically neutral, as are all celestial bodies. If protons and electrons did not cancel, and if they all had the same electric charge so that the forces were always repulsive rather than being repulsive in some cases and attractive in others, then the poster of the above fallacy would be correct: planets would be constantly trying to push themselves apart. However, this is not the case. Protons and electrons have positive and negative charges respectively so their charges cancel out in bulk matter, and electromagnetic forces can be attractive in some cases and repulsive in others.
The Electromagnetic Repulsion Myth #2
Dr. Lawrence Krauss once pointed out that if the Earth's electric charge were altered slightly (for example, by adding 1 electron for every 5 billion tons of the Earth's mass), the resulting electromagnetic repulsion would cancel out the force of gravity on an electron at the Earth's surface. Larger electric charges would theoretically overcome the attraction of gravity, and a much larger electric charge would blow the planet apart. As a result, some trekkies have decided that a low-energy electrical burst would be sufficient to destroy a planet!
However, as contradictory as it may seem, Krauss is correct but the trekkies are not. To illustrate why this is the case, I have performed my own calculations to independently verify Krauss's statements. There are two reasons to perform independent calculations here:
To test one's own knowledge level. When a well-regarded scientist makes a statement of fact regarding simple phenomena like large-scale elecromagnetic repulsion and gravitational attraction, any scientifically trained person can't help but be curious how he arrived at his figures. That curiosity often leads to an independent attempt to verify the numbers. Such attempts are not indicative of disrespect for the source of the original figures- if he is a typical scientist, Dr. Krauss would undoubtedly have no objections at all to someone independently verifying his figures, and would in fact probably be pleased that he motivated someone in this manner.
To perform extrapolations upon the original figures. It is one thing to mindlessly repeat a figure generated by an eminent scientist. It is entirely another thing to perform extrapolations and predictions based on those figures. If you understand how the figures were originally generated, you can confidently use the same method to produce other figures, for other situations. But if you don't understand how the figures were originally generated, then any attempt to generate estimates pertaining to different situations is pure guesswork.
To determine the amount of charge required to cancel out the gravitational forces acting on an electron at the Earth's surface, we can simply equate the electromagnetic repulsion force with the gravitational attraction force. Coulomb's Law of electric repulsion force and Newton's Law of Universal Gravitation are as follows:
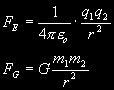
In the above equations, the epsilon term is the permissivity constant (8.85E-12 C²/N·m²) and the G term is the gravitational constant (6.67E-11 m³/s²·kg). If we take q1 and m1 as the charge and mass of the Earth, we can set q2 and m2 as the charge and mass of an electron on the Earth's surface (equal to 1.60E-19 C and 9.11E-31 kg). If we then equate the two forces, we discover an interesting phenomenon: the radius term cancels out completely! As a result, we can determine that the planetary charge q1 necessary to overcome gravitational attraction is:
![]()
It is therefore easy to substitute permissivity = 8.85E-12 C²/N·m², G = 6.67E-11 m³/s²·kg, m1 = 5.97E24 kg, and the remaining figures into the above equation to find that the electric charge necessary to overcome gravitational attraction for an electron is a mere 2.52E-7 C, which is approximately 1.58 trillion electrons. That works out to roughly 1 electron for every 3.7 billion tons of the Earth's mass. Krauss estimated the figure at 1 electron for every 5 billion tons, which means that my electron count is roughly 35% larger than his estimate. However, my figures are based on a "point charge" idealization in which all of the negative charge is located at the centre of the planet, while his figures are probably based on a uniform distribution throughout the planet. In any case, the numbers are close enough that I can confidently state that he must have used similar reasoning to mine.
Now that we have examined the reasoning behind the numbers, we can determine what they mean. Some laypeople have attempted to analyze Krauss's statements without going through all of the above work. As a result, their conclusions have invariably been flawed and sometimes comical. The following is an excerpt from a post which I received via e-mail. The original author shall remain nameless to protect his identity, since his words represent a crime against rationality:
"It would take 1.2 trillion electrons to cancel out the gravitational force of the Earth. That would correspond to an electron beam with a total rest mass/energy of 613 PeV or about 0.1 Joules worth of electrons. Ten joules of electrons could potentially blow a planet to bits. Of course getting these electrons to permeate a planet or other target would take a great deal of energy... but once present their repulsion of each other and the surrounding matter would destroy a planet."
It is hard to believe that someone could type the words "ten joules of electrons could potentially blow a planet to bits" without being certifiably insane. I can only conclude that the author of this post was either trolling, making a joke, or staggeringly ignorant. In any case, it is instructive to break down the problems with the poster's reasoning:
The author assumes that the work required to push electrons into a planetary mass cannot possibly exceed the rest mass of those electrons. This is actually untrue. The work required to push a large number of electrons into a planetary mass would be related not to the rest mass of the electrons, but to the forces of electrostatic repulsion which they would have to overcome. Think of pushing the positive pole of a huge magnet toward the positive pole of another magnet. The closer you get, the more force you will have to exert. When the problem occurs on a planetary scale, the energies and forces are appropriately large. Remember: the force necessary to overcome electrostatic repulsion is purely a function of charge, not mass. The mass of the electrons is irrelevant, as we can see by looking at Coulomb's Law which contains no mass terms.
He thinks he has hit upon yet another method of contravening Conservation of Energy. Conservation of Energy is not a legal law which can be circumvented through trickery. It is strictly observed under all circumstances, including situations of electrostatic repulsion. Although the rest mass of a set of electrons may be small, the work required to force them into a planetary mass against the force of electric repulsion will exceed the maximum amount of work that can possibly be done by their repulsion. In other words, if a large number of electrons are pushed into a planetary mass, then they will have to "climb uphill", so to speak, against their own electric repulsion to get there. The work required to do this will exceed the maximum amount of work they can possibly do to push matter outwards. Any trekkie who sets out to "disprove" Conservation of Energy is obviously either trolling (deliberately posting false information to generate controversy) or so scientifically ignorant that they should best be ignored.
Positively charged matter like protons, and neutral matter like normal bulk matter, will either be attracted or unaffected by a large negative electrical charge in the Earth's mass. If the planet were charged in this manner, it would repel negatively charged ions until the planet returns to electrical neutrality. Krauss' scenario requires that the negatively charged matter in the planet be coupled to the positively charged matter in such a way that it "pulls" the positively charged matter out of the planet with itself. Naturally, the strength of the electric charge would therefore have to be increased by the mass ratio between a single electron and the 5 billion tons of matter that it would have to "pull away" with it (which is no small ratio). This is the proportional increase that Krauss mentions, and it is far larger than the 100x increase that the author of the above post uses. Like many scientifically ignorant laypeople, he resorts to simply inventing a number quite literally out of thin air if he doesn't know what to do, hence the arbitrary 100x multiplier to get his 10J figure. Of course, none of this would actually ever happen because of the nature of electrostatic repulsion, which is why Krauss doesn't actually pretend that the scenario is realistic- it is merely a visualization tool to explain the relative strengths of elecromagnetism and gravity. He never would have imagined that some trekkie would misinterpret his work as a method for contravening Conservation of Energy!