Basic Calculus: Integration

Written: 1998.10.31

For those who are not familiar with basic calculus principles, integration is the opposite of differentiation. The differential of a function is the instantaneous slope of that function, for any given value of its independent variable. The integral is the opposite: it is used to evaluate the absolute magnitude of a function, for which the formula is unknown but the differential, or slope, is known. When we integrate a function, we evaluate its magnitude from its slope (note that an initial value is also necessary). When we integrate a function over a range, we are evaluating the "area under the curve" (in this case, an initial value is not necessary because the initial values cancel when you subtract the low-range value from the high-range value). For example, most of you learned in school that the volume of a sphere is V=4/3πr³. However, those of you without calculus training may not realize that this formula can be easily derived by simply integrating the spherical surface area function A=4πr² from the centre of the sphere to its full radius. The example of integrating spherical surface areas through radii is of particular interest, because it can be directly applied to the problem of planetary gravitational binding energy.

Another way of describing integration is that it splits large tasks up into small tasks. As an example, let us examine a line graph of the simple function y = 60-(x-10)²:

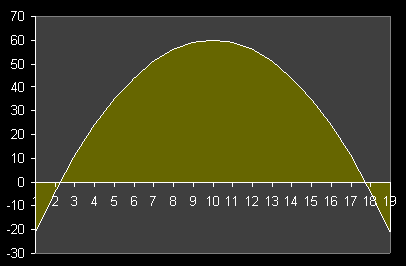
In this chart, we can see the usual inverse parabolic shape that one would expect from this function. The area under the curve is highlighted in green- note that some of the area is actually negative. If you wanted to measure the area under this curve, you would have to subtract the negative portions from the positive portions. How do we determine this area? We integrate the curve function from x=1 to x-19, and the result will be the area. When we integrate, we are essentially slicing up the parabola into an infinite number of thin vertical slices, or bars. The area of each bar is then calculated, and the values are added up. We obviously cannot show the above formula being sliced into an infinite number of bars, but we can illustrate the concept by using wide, easily discerned bars:

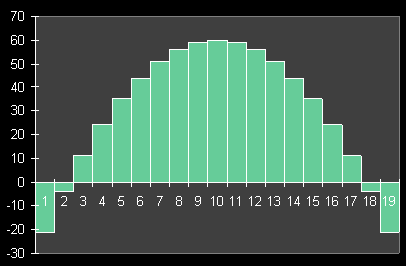
If we calculate the area of each bar and add them up (making sure to count the negative bars as negative areas), we can generate an area estimate of 570. Of course, since we are using large blocky bars rather than a smooth integration, this answer is not very accurate. If we used bars that were half as thick, we would have twice as many bars (and twice as much work), but we would get a more accurate result. When we perform an analytical integration, we are using an infinite number of infinitesimally thin bars, to achieve the greatest precision possible. This is what the analytical integration looks like for the preceding function:

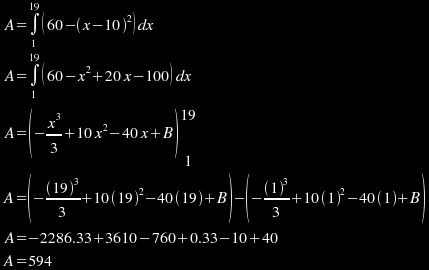
Notice how the result is different. This result is considered precise because it was derived through "analytical methods" as opposed to "numerical methods" (adding up the bars in the bar graph), and analytical methods determine the limit of the sum as the bar width approaches zero. Computer software generally uses numerical methods rather than analytical methods because computers aren't smart enough to perform analytical calculus. But even if they were, there are sometimes equations which are so complex that they cannot be solved analytically, and you have no choice but to solve them numerically. Computers attempt to approach the accuracy of analytical methods by using very small steps, but this approach is limited by CPU power and rounding error (if the bars are made too small, the limited precision of floating-point calculations in a computer CPU will introduce too much "noise" into the process and cause the result to be less accurate).

In short, the numerical answer will always have limited accuracy compared to the analytical answer, which is the price you pay for the relative simplicity and lack of skill required. This is why mathematicians will always prefer the analytical answer, and even scientists and engineers will prefer the analytical method if it is feasible.

Thus endeth the basic calculus lesson. If you don't understand the above equations, don't worry; the point is that you should understand the basic concept, even if you don't understand the mathematics behind it. As long as you understand that integration is essentially the "slicing into small pieces" method applied to infinitely small slices, then you will understand the basic idea used for integrating Newton's gravitational potential energy formula from the centre of a planet to its surface.