Size Matters
Yes, size does matter, and it doesn't matter whether you like that or not. It's a reality of life, and you'd better get used to it. Here are some tragically commonplace misconceptions:
"Huge sci-fi ships don't necessarily mean high technology."
"Huge sci-fi ships only mean that they have lots of raw materials."
"The Federation could easily build huge ships if they wanted to."
"Smaller ships are more advanced because they're miniaturized."
Does that sound familiar? Sure it does. It's the "size doesn't matter" argument, and you've heard it a hundred times before. But size does matter. A 60km long ship must be a hundred times stronger than a 600 m long ship even after accounting for the size difference, and I intend to explain why.
Stress
Before I begin, I must explain what stress is. Mechanical stress (as opposed to psychological stress) is expressed in units of force divided by area, and it is conceptualized as the load acting normal to a plane surface, divided by the area of that plane surface. If I just lost you, then perhaps the following diagram will help you visualize the idea:
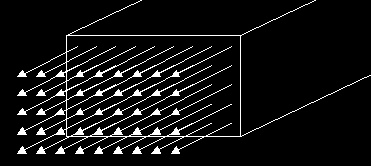
The diagram shows a bar which is being stretched. We call this "tensile stress", and it's the simplest possible situation in stress analysis. The little arrows show the force acting on the bar, and of course, it's spread out over the entire area of the bar's cross-section. This cross-sectional area is often referred to as the "load-bearing area". For example, if the load-bearing area is 5 m² and the bar is supporting a 100,000 ton mass against the force of gravity, then the stress would be roughly 2E8 N/m², or 200 MPa (structural steel yields at ~260 MPa, in case you're wondering).
The critical factor is the load-bearing area. The length of the bar doesn't help at all, and you can verify this with an experiment. Get a length of good high-quality rope, tie one end to a solid post, and try to pull on the other end until it breaks. Does it matter how long the rope is? No. You could cut a 100 foot length and it would be no stronger than a 1 foot length. So the moral of this story is that the load-bearing capacity of our bar is affected by changes in width or height, but not by changes in length. If you scale the bar up by a factor of 100, then its volume will increase by a factor of 1 million but its load-bearing area will only increase by a factor of 10,000.
So Why Does Size Matter?
Ask the nearest female :) But after you get your answer, try to remember that size matters from an engineering standpoint which has nothing to do with impressing women. Size matters because of gravity and acceleration. If you're building an immobile space station in a zero-gravity environment (such as the Borg headquarters array, a Federation starbase, or Mir), size doesn't matter. But if you're building a ship, then things become a whole lot more complicated. When that ship accelerates or enters the gravity well of a planet, the resulting forces will be proportional to its mass. Its mass, in turn, is proportional to its volume.
It doesn't take a genius to see the problem here: when you scale something up, the mass increases faster than the area. Mass will define load, and area will define load-bearing ability. If load increases faster than load-bearing ability, then we have a problem. For example, if you scale up a building by a factor of 10, it will get 1000 times heavier but it will only get 100 times stronger.
This problem isn't restricted to stress analysis; technological devices which apply force also don't scale with volume. For example, a hydraulic cylinder's maximum force is dependent on the piston area, not its volume. If you take a hydraulic cylinder and precisely scale it up 10 times in every direction, it will be 1000 times more massive but it will only exert 100 times more force. The same is true of biological systems such as muscles, for which the predominant strength determinant is cross-sectional area.
In general, if you scale up an object, its strength will increase with the square of the size multiplier, but its mass will increase with the cube of the size multiplier. That's why Galileo knew, many centuries ago, that there's a "proper size" for everything. You can't scale something up without radically altering the design, and when the size of an object reaches extreme levels, it becomes infeasible regardless of design.
Case Study: The Egyptian Pyramids
The pyramids are often used as "proof" that you don't need a lot of technology to make a really big building. However, nothing could be further from the truth. They represent a fascinating study in ancient ingenuity and precision stone-cutting techniques, but that's all they represent.
The Great Pyramid at Giza is the largest and most famous of the Egyptian pyramids. Its sides are sloped at roughly 52° and it stands roughly 140 metres tall. Its mass is estimated to be around 5.25 million metric tons. That may sound impressive (so much so that pseudoscience types spout the usual "alien visitation" theories about its origin, often buttressing their argument by exaggerating the precision and difficulty of its construction), but remember that their builders had to make three huge compromises:
The pyramid shape, which was not a purely aesthetic choice. It was a concession to their poor building materials. A building of that size, constructed primarily out of soft limestone with a decorative granite shell, would never have survived if not for the pyramidal shape. It was also the only shape they could build on that scale with their limited construction technology.
The paucity of internal spaces. This was also a concession to their limited technology; the vast pyramids had only a handful of internal chambers and tunnels, quite unlike the airy interiors of modern office buildings or even the interior of a typical Egyptian home dwelling of that era.
Time and money. It took an estimated 30 years for 20,000 labourers to build the Great Pyramid. If we convert this to modern terms, assuming a 5-day work week and a paltry $10/hr rate of pay, the labour costs alone would exceed ten billion dollars, to say nothing of the material costs.
Why a pyramid? The pyramid shape provides a large load-bearing area where it's needed the most: at the bottom. Pyramids have some interesting characteristics:
87.5% of the mass is in the lower half. That's the geometry of pyramids; the volume of any pyramid is proportional to h³ (in this case, it would be roughly 0.81h³), so the upper half is only 1/8 of the total volume.
The base area for a pyramid with 52° sloped walls is roughly 2.44h², or 48,000 m² in the case of the Great Pyramid. This means that its 5.25 million ton mass is distributed so that the average ground pressure is less than 1.1 MPa. By way of comparison, modern structural steel yields at ~260 MPa.
If you were to take the pyramid and reshape it into a 75 metre wide square building, it would be 400 metres tall (almost as tall as the Sears Tower in Chicago). Its base would take 8½ times more stress than the pyramid, but the compressive strength of limestone is actually high enough to withstand this. The problem is that they couldn't build it, and it wouldn't hold together if they did. They used ramps to slide the blocks up to the top levels of their pyramids, but how would they lift these blocks to the top of a square building? And while a pyramid is an easy loading scenario, how would a 400 metre tall limestone rectangle survive high winds? Wind creates a complex shear, tensile, and compressive loading scenario on a tall skyscraper, and limestone doesn't handle the first two types of load very well at all.
Pyramids and cones are the easiest, most natural shapes to project out of the ground. If you want to test this claim, simply go to the beach and try to build a huge pyramid, followed by a skyscraper of equal size. Which one is more durable, and easier to build? If you're working with soft materials, a pyramid is the only way to go.
So could the Egyptians scale up a small structure into a big one? Most certainly not ... their small strucrtures had a wide variety of shapes and designs, most of which were not pyramidal. But when they tried to make a large structure, they were forced into the pyramidal shape. In short, the design of the pyramids was driven entirely by their scale.
Even if we ignore the limitations of Egyptian construction techniques, we can easily determine that their construction materials would never support a modern skyscraper. Modern skyscrapers subject their structures to far more stress than the pyramid structure had to handle, because they support their weight on relatively small load-bearing supports rather than huge solid regions. Furthermore, that stress will be a combination of tension, shear, and compression as the building resists gravity and wind. Limestone, on the other hand, has middling compressive strength but it suffers from poor shear strength and almost no tensile strength (a common failing of ceramics), because it isn't anisotropic (insensitive to direction of load) like structural steel.
Contrary to the beliefs of some superstitious mystics, the pyramids don't represent unthinkable engineering skills on the part of the Egyptians or their imaginary alien benefactors. In fact, the pyramids show us their limitations in stark detail because those limitations drove the design, both in the area of construction technology and materials science. They're not examples of huge, ancient buildings; they barely qualify as "buildings" at all. A building is normally expected to be largely hollow, consisting mostly of habitable spaces. Houses qualify. Skyscrapers qualify. Even military bunkers qualify. But the pyramids do not. They're giant glorified rock piles, not "buildings" in the traditional sense.
Case Study: The Dyson Sphere
"That's all well and good", you might say, "but this is a sci-fi website, not an ancient history website." True enough, so let's leave the dreary Egyptian desert and boldly go where no man has gone before. First stop: the Dyson Sphere. The Dyson Sphere was a spectacularly massive structure. In fact, it is the most massive structure I can recall seeing in sci-fi, even bigger than Unicron or any of the mighty worldships of Galactus. It was featured in the TNG episode "Relics", and no one knows who built it, or how old it is. The only thing we do know is that its builders must have wielded forces and engineering skills far beyond any of their counterparts in the Star Trek universe. Contrary to certain popular (albeit painfully simple minded) beliefs, the difficulty of constructing such a vast structure does not end with the procurement of the necessary raw materials.
This is a spherical shell with 100 million km radius. Let's imagine that its wall thickness is 2 km, and its shell has the same density as iron (yeah, I know, it's suposed to be "carbon neutronium", as if it makes sense to combine a lightweight element with superdense degenerate matter). Anyway, the mass of an iron shell would be roughly 2E30 kg, or one solar mass! Not only is this an absolutely staggering amount of resources to call into action (it suggests they'd be able to build stars at will, in places of their choosing, since they can summon up solar masses of engineering materials), but it would require staggering material strength.
It is tempting to imagine that it is rotating about its axis to generate artificial gravity, but if that were so, the resulting centripetal force would be unsuitable for the creation of a uniform M-class environment on the sphere's interior. The problem is that if we visualize the axis of rotation as vertical, then the centripetal force will be horizontal. At the equator, this will work perfectly. But if we move away from the equator toward the poles, we will see that direction of the centripetal force vector diverges farther and farther away from the "surface normal" of the sphere. In other words, as your latitude increases, the proportion of the centripetal force that acts like gravity will decrease, and the proportion of the centripetal force that slides you sideways along the surface (toward the equator) will increase, as shown below:
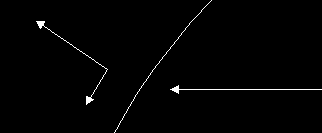
One look at the diagram and the problem should be obvious: all of the atmosphere, oceans, and other surface material will eventually end up in a thin band around the equator of the sphere. This is obviously unacceptable; there's no point building such a huge structure if 99.9% of it will be uninhabitable. Unlike Niven's far more realistic Ringworld, the Dyson Sphere cannot possibly generate its surface gravity through rotation. Therefore, the Dyson Sphere must have near-zero angular velocity in order to keep from pushing all of its material toward its equator, and it must use something other than the centrifuge principle to generate its artificial gravity.
So if there is no centrifuge stress, would there be any stress? The answer is yes, because an object of such stupendous size will generate significant gravity, which will add to the existing gravity of the star at its centre. Since the sphere's radius is only 2/3 of an A.U., its sun would have less than half of our Sun's luminosity (or the oceans on the sphere's inner surface would have evapourated), so it would probably have less than half our Sun's mass as well. This means that its mass is roughly 1E30 kg.
From an engineering standpoint, the Dyson Sphere can be thought of as a thin-walled spherical pressure vessel, and the gravitational force can be thought of as the "pressure" (once it's divided by the internal surface area, of course). The mass of the sphere is 2E30 kg, the mass of the star is 1E30 kg, and the radius is 1E11 m, so Newton's law of gravitation gives us 1.33E28 N. The internal surface area of the sphere is 1.26E23 m², so the equivalent "pressure" would be roughly 106 kPa.
Now, that's not a lot of pressure (it's roughly 1 bar), but it's acting over an enormous surface, and that comes into play when you try to calculate the resulting stress in the sphere wall. The equation for in-plane stress in a thin-walled spherical pressure vessel is pr/2t where p = pressure, r = radius and t = shell thickness, so the tensile stress on the shell would be roughly 2.65 TPa! To put this in perspective, it's roughly ten thousand times the yield strength of structural steel. Not bad, eh? It's also insensitive to the exact wall thickness of the sphere, because a thicker wall will increase the load-bearing area but it will also increase the mass of the sphere and hence the load (a full derivation would show the wall thickness term cancelling out).
As if it isn't enough to need steel which is ten thousand times stronger than normal, we still have to consider the construction problem: how would you build such a beast? A full sphere would have at least twice the mass of the star but the effect of its gravity on the star would be symmetrical and therefore nullified, so that the star isn't disrupted. However, what if they've got only one quarter of the sphere done? That would pull the star to one side, severely disrupting it in the process. They would have to carefully balance the construction of countless trillions of balanced segments around the star as they build the sphere so that symmetry is preserved at all times, and they would have to use huge engines to hold these pieces in place until they can be joined together into the finished sphere.
We can build a ping-pong ball today, but that doesn't mean we'll ever be able to build a Dyson Sphere (although, to be honest, Ringworld is a much better idea anyway).
Case Study: B-movies
I don't know about you, but I miss B-movies. When I was a kid, they would show these cheesy 1950's and 1960's sci-fi horror films on late-night TV, along with those wonderfully cheap kung-fu movies, bad dubbing and all. I still remember getting together with a good friend and staying up late to watch those crappy films, surrounded by buckets of junk food and pop. Alas, local television stations don't show that stuff any more, because they discovered they can make more money by showing those damned infomercials. After midnight, the tube is dominated by psychic hot-lines, cheesy mail-order products, and get-rich quick schemes ... a fine justification for capital punishment if I ever saw one.
Anyway, enough off-topic ranting for now. One thing about those old movies is that they were entirely preoccupied with size. Everywhere you looked, you would see creatures transforming or mutating into huge versions of themselves. Giant insects scaled buildings, Godzilla stomped Tokyo, and 50 foot women walked the Earth (complete with enlarged clothing and makeup). Ahhh ... now that was entertainment! Did any of this make sense? Of course not. But the realism problems didn't stop at the biological limitations that everyone knows and loves. People rarely ask themselves if these giant creatures would be structurally sound, and the answer is that they aren't. Let's look at a few examples:
Giant Insects
One of the mainstays of the classic B-movie era was the giant insect. Maybe there's something about giant insects that touches a primordial fear in all of us, or maybe they just made those movies because the special effects were easy to do. Either way, the image was a lasting one, and it still survives to this day, in the form of big-budget gorefests like "Starship Troopers".
Now, we all know that a bug's circulatory system can't be scaled up to enormous size, but what about its legs? Its wings? Its exoskeleton? Would they be able to stand the weight? People love to point out that an ant can lift 50 times its own weight, while a human can barely lift one times his own weight. As the saying goes, "if an ant were scaled up to the size of a human, he would be able to lift 7500 pounds!"
However, while the original observation (that an ant can lift 50 times his weight) is correct, the conclusion (that a human-sized ant would be able to lift 50 times his weight) is completely wrong. Just as the stress in a building's structural members is controlled by the ratio of load to cross-sectional area, the strength of animal muscles is predominantly controlled by their cross-sectional area.
Let's take an ant which is 5mm long, and enlarge it to about 1.7 metres long, like an average human being. Since the ant becomes about 340 times longer, it must become about 40 million times heavier, since mass is proportional to volume. However, the cross-sectional area of its legs would only be roughly 115,000 times bigger, so it would be 115,000 times stronger and its legs would be subjected to roughly 340 times as much stress. Proportionally, it will be 340 times weaker than it was at its "correct" size.
Therefore, while an ant might lift 50 times its own weight, if you scaled him up to human size, it would only be able to lift 0.15 times its own weight. This is like a 150 pound human being who struggles to lift a 20 pound dumbbell with both arms! That's utterly feeble, and such a feeble creature would most likely not be able to stand on its own power.
So if a human-sized ant might not even be able to move about on its own power, what about those huge building-sized ants in the B-movies? Try making our human-sized ant 20 times bigger. Now, the ant that could should lift 50 times its own weight would be limited to 0.007 times its own weight. This would be like a 150 pound human being who struggles to lift one pound! That's not even enough to survive. An ant of such size would collapse, its exoskeleton shattering like cheap glass, its eyes collapsing of their own weight and its internal organs rupturing spontaneously and spilling their fluids onto the ground.
The biologists criticize the giant-ant movies by saying that their circulatory systems wouldn't work, but the structural engineers can beat them to the punch: the giant ants won't get a chance to asphyxiate because they'll collapse into a puddle of goo first.
The 50 foot tall Woman
Did anyone else ever see these movies? It was almost a genre at one point, with huge people walking around all over the place. The structural problems faced by a huge person are similar to those faced by a giant insect:
A 50 foot woman would have nearly 10 times the height of a normal woman. If we assume the multiplier to be exactly 10 (for the sake of mathematical simplicity), this means she would weigh 1000 times as much as a normal woman, but the cross-sectional area of her muscles and bones would only increase by 100 times, so her bones would be subject to ten times more stress than normal. Normal adult humans can range in weight from under 100 pounds to over 1000 pounds so the skeleton wouldn't shatter under gravity, but acrobatic movements would be out of the question.
Since human muscle strength is proportional to muscle cross-section area, she would have only one tenth her normal strength. This wouldn't be enough to kill her, but movement of any kind would be very laboured.
Fluid systems are controlled by pressure, and pressure is proportional to area. Her heart would pump blood through her arteries at one tenth its normal pressure (because the heart is a muscle), and her veins would return blood at ten times their normal pressure (because the ratio of blood mass to vein cross-section area will be ten times greater). In other words, she'd have double trouble: the blood will pool around her ankles and her heart won't be able to pump it back to her head.
The first two problems would be severe nuisances, but the third would undoubtedly be fatal. Although I'm not a doctor, I can't imagine that 10% blood pressure in the arteries and 1000% blood pressure in the veins would be a long-term sustainable situation. The 50 foot woman should have died. It's as simple as that. Also, her high heels should have collapsed under the weight, and her clothes should have shredded easily as she moved around in them (which would have made the films more interesting if not for her quick death).
Godzilla
Hey, what discussion of B-movies would be complete without the almighty Godzilla? You can't help but love the big guy ... he crushes buildings, he has fire breath, and he shakes off artillery like a gentle rain. What's not to love?
But would he hold together? Godzilla has varied in size over the years, but let's look at his huge, 100 metre tall early 90's incarnation. That huge Godzilla is around 60,000 tons by most accounts, and if you scale him down to human size (accounting for his bulky shape) this figure seems plausible.
Now, would he hold up? When he stands, all of his weight rests on the bones in his legs. If we use the proportional thickness of the human femur as a basis for comparison, he would have to support his enormous weight on bones which have 3.5 m² of cross-sectional area at their narrowest point. And here's the bad news: 60,000 tons supported by 3.5 m² works out to a compressive stress of more than 170 MPa, or nearly twice the ultimate compressive strength of bone (note that I'm not even accounting for the fact that he can walk and jump, which will produce much higher stresses than merely standing still).
Moral of the story? Godzilla shouldn't survive. His bones should shatter, his epidermis should rip open like an overinflated water balloon, and his guts should spill all over the streets of Tokyo. Alternatively, if we decide to suspend disbelief, we can only look at him and speculate that he must have bones of structural steel and skin like armour plate. Oddly enough, this means that the more "realistic" fleshy and vulnerable Godzilla in the recent Matthew Broderick film is actually less realistic. If Godzilla exists at all, he must be quite literally built like a tank.
All hail Godzilla! King of the monsters.
Case Study: The Executor
Executor-class star destroyers are good examples of the engineering difficulties posed by large-scale starship construction. Let's look at the specs:
Length: 17.6 km
Width: ~6.5 km
Thickness: ~1.7 km
The Executor decelerated at a rate of roughly 30 km/s² in ROTJ along with the rest of the fleet, so what kind of force would be required? If we assume 10% solidity and iron construction, the ship's mass would be well over 35 billion tons. In order to accelerate that much metal at 30 km/s², its 13 engines would have to generate around 8E16 N apiece. If I recall correctly, each engine is perhaps 300 metres wide, so the outlet pressure would be around 1.13 TPa. An engine of such outlet pressure, scaled down to a pair of 10x10 metre squares and attached to the back of, oh, say, a 4.5 million ton starship would accelerate it at more than 50,000 m/s².
Even if we ignore the engines and look only at the structure of the ship itself, it would have to be enormously strong in order to simply survive this rate of acceleration. Let's take its cross-sectional area at the thickest point to be roughly 5.5 million m². If the ship is 10% solid, this would mean there is roughly 550,000 m² of metal which has to withstand a total of more than 1E18 N of force, for a resultant stress in excess of 1.8 TPa (nearly 7000 times the yield stress of structural steel). In fact, even if it were a solid block of metal, it would still have to be made out of a material which is 700 times stronger than structural steel in order to survive the acceleration without permanent deformation!
We also know that the Executor can survive the gravity of a planet even when it's powered down, because an Executor-class ship was buried for years under a mountain range on Coruscant. However, the stresses imposed on its frame from its high sublight acceleration would be much higher than the stresses imposed by the weight of a mountain range, so the ship's ability to survive its own engine output is still its most impressive attribute (particularly during hard turns such as the one in ROTJ, which would impose bending moments on the ship's frame). It must be constructed out of impossibly strong materials or it must incorporate some sort of forcefields in order to hold it together.
Case Study: The Death Star
If we're talking about big Imperial starships, we can't go away without mentioning the Death Star. Contrary to popular belief (and Obi-Wan Kenobi's statement to the contrary), the Death Star is actually a starship rather than a battle station. Remember that a battle station is, by definition, stationary, while the Death Star was able to easily traverse many tens of thousands of light years in a matter of hours, under its own power. Now let's look at the numbers:
Diameter: 160 kilometres
Maximum sublight acceleration: at least 1 km/s² as demonstrated in "Star Wars: A New Hope"
Armament: tens of thousands of heavy turbolaser turrets, and one planet-destroying superlaser
The structural stresses imposed upon the Death Star during its 1 km/s² acceleration are huge. Let us imagine that the Death Star's interior is 10% solid, and composed of iron. This would give it a mass of 1.7E18 kg (a very conservative figure since it unleashes energy with a mass-equivalent of around 1E21 kg when it destroys Alderaan). Its sublight engines are distributed around its equator, but only half of them can possibly fire in any given direction at once. They are invisibly small from a distance of only a few kilometres away, so it would be extremely generous to assume that they are ½ km wide apiece (let's say they're round).
If there are 200 such engines spaced around the Death Star's equator, and half of them fired to accelerate the station at 1 km/s² in ANH, each engine would have to exert 1.7E19 N of force. Given the (ridiculously exaggerated) ½ km diameter of each engine, that would work out to very conservative 87 TPa. This would, of course, also be the bearing stress on the back of the engine (and it's more than 300,000 times the yield stress of structural steel).
How potent would these engines have to be? Let's put it this way: if you took an engine of such nozzle pressure, and scaled it down to 1 metre wide (like one of the engine outlets on an F-15 Eagle), it would produce enough thrust to accelerate the 21 ton aircraft at roughly 330 million g's! Those pilots stay in pretty good shape, but I think that would turn even the toughest aviator into a pile of goo.
What about a certain fictional starship, rumoured to be about 4.5 million tons in mass? Let's take our 87 TPa engines, scale them down to a pair of 10 metre wide squares, and put the pedal to the metal. How fast will it go? Try 3.9 million m/s². The Death Star is famed for its ridiculously powerful weapon, but its frame and its engines are rather impressive in their own right.
The lesson from the examples of the Executor and the Death Star is clear: in order for a huge starship to accelerate at great speed, its frame and its engines must be much stronger than those of a small ship, even after accounting for the size disparity.
Conclusion
When some simpleton looks at enormous sci-fi structures and concludes that anyone could build them with enough raw materials, he is only betraying a pitiful lack of engineering knowledge, not to mention common sense. Have you ever seen the Tonka commercial where they shove a Tonka truck and real, full-size dump truck off a cliff? The Tonka truck bounces and clatters all the way down to the bottom, dented but intact. The full-size dump truck, on the other hand, crashes to the bottom as a twisted, barely recognizable pile of wreckage. The humourous subtext to the commercial was that Tonka trucks are tougher than the real thing, but the real story is as an object grows larger, its own mass becomes its worst enemy.
As an aside, this is one of the problems with automotive crash testing. By slamming a car into a nigh-immovable concrete wall or barrier, the NHTSA artificially elevates the crash-test scores of small cars while artificially depressing the scores of large cars. In a collision with a barrier of effectively infinite momentum (by virtue of being anchored to the ground), a large car will be crushed by its own weight. But in a collision with another car, the situation is entirely different. The car with lower momentum will suffer greater deceleration and hence, more damage. That's why sub-compacts score well in crash tests but fold like cheap tents in real-world crashes (the lethality of SUV's in collisions is partially due to their superior mass as well, but it's also due to their high bumpers which tend to crash through car windows, thus giving us yet another reason to consider raised SUV suspensions incredibly irresponsible).
Anyway, back to the subject at hand: you can't just "scale up" a design to make a bigger building or a bigger ship, even if you have the necessary raw materials. Bigger designs require entirely different engineering and construction methods, not to mention superior materials. Every time I get an E-mail from some dumb-assed Trekkie who says "the Federation could build a Death Star if they wanted to; it's just a matter of raw materials" (especially from the pin-heads who cite the Egyptian pyramids as proof), I'm reminded yet again that common sense is nowhere near as common as one might hope.
Acknowledgements
Brian Young, for valuable feedback on some physiology questions.
Mike Johns, for noticing an error in my momentum/driving analogy.